
 | |
  nagazeli.ru |
Архитектура -> Фермы, арки, конструкции геометрические расхождения. Данный тип оболочки и.меет много общего с куполах»! - ее зачастую можно представить как купол с отсеченными сегментами, представляющий иространсгвенную форму, опирающуюся в четырех углах. Тонкостенная оболочка опирается по контуру на жесткие поддерживающие конструкции - диафрагмы, роль которых выполняют арки, сетментные фермы, криволинейные балки, стены с закругленными фронтона.ми (рис. 10.2). Диафрагмы работают с оболочкой совместно, воспринимая усилия сдвига, развивающиеся по ее контуру. Расчет оболочки Для покрытий чаще всего применяют пологие обо.точки, что определяется удобство.м изготовления и условиями возведения. Существуют два вида расчетов пологих оболочек: предварительные, упрощенные - Д.ЛЯ оценки технических решений и вариантов конструкции и рабочие - .Д.ЛЯ решения конкретных задач проектирования и обоснования рабочих чертежей. В первом случае расчег оболочки может произво.лнться по безмомент-ной теории, во второ.м - по момеитной теории. При расчете пологой оболочки переноса используется ряд допущений: в частности, она рассматривается как слегка искривленная пластинка; геометрия срединной поверхности за.меняется геометрией на плоскости, в силу этого длину элемента оболочки приближенно принимают равной его проекции на плоскость плана; влиянием гауссовой кривизны, вследствие ее малости, пренебрегают. Вместо криволинейных координат используются ортогональные координатные линии. Материал оболочки считают однородным, изотропным; вертикальную, равномерно распределенную нагрузку принимают нормальной к поверхгюсти. На основании введенных предпосылок расчет оболочки значительно уирощаегся. Безмоментная теория построена на предиоложении, что в единично.м элементе оболочки действуют только нормальные Ny и касательные Ny силы, которыми преимущественно и уравновешиваются внешние нагрузки, а изгибающими, крутящими моментах™ и поперечныхщ силами, вследствие их малости, пренебрегают (с.м. рис. 10.1 б). В оболочках, за1Д)уженных равномерно распределегшьтми нагрузками (собственный вес, снег), в значительной их области возникает безмоментное напряженное состояние, а моментное - в местах примыкания обо,лочки к контурным конструкщмм, резкого изменения нагрузки или кривизны иоверхности и в зоне приложения .местных нагрузок. Поэтому 80...90 % площади обо,лочки испытывает лишь действие сжимающих сил. Безмоментная теория с учетом изгибающих моментов, возникаюищх в при-опорных зонах, может быть использована в предварительных расчетах шарнир-но-оиертых гладких оболочек при равно.мерно распределенной нагрузке. В рабочем проектировании пользуются методом расчета на основе моментпой теории, учитывающей конструктивные особенности оболочек: ребра, отверстия, переломы поверхностей, тип контурной конструкции и т.п. Стандартные программы расчета по моментной теории позволяют получить довольно точное решение. Справочные материалы в виде графиков и таблиц существенно облегчают процесс статического расчета оболочки. Д.ТЯ вычисления усилий пользуются уравнением равновесия без%юментного напряженного состояния пологой оболочки при равно.мерно распределенной нагрузке f: k ,N, + 2k,yNxy + kyNy = -q, (10.2) где ,тля эллиптического парабо.тои,1а параметры к= 2/ / а: ку = 2/у/ Ы и ку = О (оси координат совпадают с направлениями главньгх кривизн оболочки). Нормальные Ду.. Ny и касательные усилия записываются с помощью функции напряжений, которая может быть выражена алгебраическими, тригонометрическими полиномами и должна удовлетворять одновременно условию равновесия оболочки и граничным условиям задачи. Зная функцию напряжений, определяют значения виутренни.х усилий в любой точке оболочки [6]. Главные растягиваюптие усилия jV,„, и главные сжимающие усилия j¥„,c находят по формулами = fNx+ Ny)/ 2± Ny f /4 + Ny (10.3) Полученные эти.м методом эпюры усилий в основных сечениях оболочки позволяют оценить ее напряженное состояние. Для однопролетной оболочки с квадратным планом при равных постоянных кривизнах в обоих направлениях и равномерно распределенной нагрузке, т.е. при а = Ь: fp=ff=f: Rp= Д,= R: Ад.= Л,= lf/a-=\/R и q = const, значения усилий в отдельных точках оболочки могут быть определены но эпюрам, представленным на рис. 10.3. При этом предполагается, что контурными конструкциями могут служить железобетонные криволинейные балки, стены, фермы, арки с развитым верхним поясом. Они обладают достаточной жесткостью в своей плоскости и могут считаться практически недеформируехил.ми вдоль сторон контура. На контуре оболочки нормальные усилия = О ввтгду податливости опорной диафрагмы из своей плоскости. Здесь же усилия Ny = О, поскольку оболочка не может деформироваться вдоль контура вследствие значительной его жесткости. Нагрузка передается на диафрагмы силауит сдвига Ny Из графиков видно, что бо.льшая часть оболочки подвержена сжимающим уси-лия.м в двух взаи.мно нерпендикулярных направлениях (область двухосного сжатия). В центре оболочки нормальные усилия (кН/м) в обоих направлетшях равны: = Лр = - 0,5 qR. На расстоянии, приблизительно равном 114 I, = - 0,87 qR. В угловых зонах возникают наибольшие усилия: в одном направлении (от центра к углу) - главные сжимающие (N. = ~l,35qR), в другом (по нормали к ним) - главные растягиваюише (N„, = + \ .35qR). Сдвигающие усилия на контуре имеют .максимальные значения также в углах (Л, = -1,35й) и равны нулю в середине -0.87qRSZ a=b , a=b a=b a=b 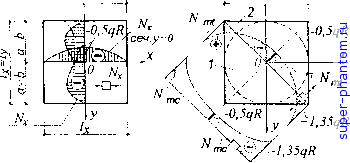 Qi-сжатие; ф-растяжение -l,35qR a=b . a=b Л
N,35qR сечх=а Рис. 10.3. Эпюры усилий в пологой оболочке, квадратной в плане: а - усилия У для сечений х = О, у = 0: б - главные усилия N„, и для сечения х = у, в - усилия Nx, для сечения х = а н моменты в зоне местного изгиба у контура оболочки; / - область двухосного сжатия; 2 - область сжатия в одном направлении, растяжения - в другом. (Эпюры усилий аналогичны jVv , но в плане повернуты на 90°) сторон контура вследствие симметрии оболочки. Все внутренн1ю усилия вычисляются для элемента оболочки размерами 1х1м. Пологую оболочку переноса можно также рассчитать приближенным методом, предполагая, что она является элементом сферы. Отсекая в центральной зоне горизонтальной плоскостью часть оболочки и рассматривая ее в равновесии, определяют внутренние усилия. При этом сохраняется вполне удовлетворительная степень точности результатов вычислений, за исключением контура покрытия, где напряженное состояние оболочки существенно отличается от купола [5], [15]. Изгибающие моменты в приопорных (контурных) зонах невелики, но ири конструировании они учитываются {см. рис. 10.3 в). Действующий в зоне местного изгиба на расстоянии от края х - 0,579 л/к7 момент равен: M„ax== 0,0937qRt, (10.4) где Rut - соответственно, радиус кривизны и толщина оболочки. Устойчивость оболочки считается обеспеченной, если интенсивность расчетной нагрузки не превыщает критической величины: q„=Efi /(2()RRy), (10.5) где Лд. п Ry - радиусы главных кривизн 1Юверхности; Е - модуль упругости материала. Усилия в основных элементах диафрагмы могут быть определены по формулам: в нижнем поясе фермы или затяжке арки Рн.п = ч1П24/к (10.6) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 [ 25 ] 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |